
Question1: A person going on morning walk at 6 am. He went a certain distance on level ground at 4km/hr. then he travelled certain distance uphill at 3km/hr. and a certain distance downhill with 6km/hr. After reaching there he turned back and returned to the starting point and when he saw his watch its 12noon. Find the total distance travelled by him.
Solution: Let the distance on the plane ground, uphill and downhill be d1, d2, d3 respectively.

Their speeds are given as: Level ground i.e. D1 = 4 km/hr., Uphill i.e. D2 = 3km/hr. and Downhill i.e. D3 = 6km/hr.
At the time of returning the speed for D3 = 3km/hr., for D2 = 6km/hr. and for D1 = 4km/hr.

So, total distance travelled is equal to 12✖2 = 24 km.
Here we will study 4 cases. And almost all train related questions are based on these 4 concepts only in our exam.
Let the length of the train be ‘l’, the length of platform or, object be ‘l0’.
The speed of train be ‘s’, the speed of object be ‘s0’ and time be ‘t’.
CASE 1: Static Object with no length.
Here speed of object = 0 and length = 0. And since we know that distance = speed ✖ time. Then,

So, total distance travelled is equal to 12✖2 = 24 km.
Concept: How to solve Train Related Questions.
Here we will study 4 cases. And almost all train related questions are based on these 4 concepts only in our exam.
Let the length of the train be ‘l’, the length of platform or, object be ‘l0’.
The speed of train be ‘s’, the speed of object be ‘s0’ and time be ‘t’.
CASE 1: Static Object with no length.
Here speed of object = 0 and length = 0. And since we know that distance = speed ✖ time. Then,

Here speed of object = 0 and length = l0. Then,

CASE 3: Moving Object without length.
Here speed of object = s0 and length of object = 0. Then,

if the train and object are in same direction the use ‘-’ sign.
CASE 4: Moving Object with length.
Here speed of object = s0 and length of object = l0. Then,

if the train and object are in same direction the use ‘-’ sign.
Question2: A train having length 500 m crossed a man standing on the platform in 20 seconds. And the same train crosses the platform in 90 seconds. Then find the length of the platform.
Solution: This is clearly the concept of two things i) static object without length and then for finding the length it is the case of ii) static object with length. Here length of train = 500m. Then,
Speed of train = 500/20 = 25 m/sec. Now,

Question3: There are two trains one is having length 200m and the other is having 400m length. When they are travelling in opposite direction it takes 15 sec to completely cross each other while travelling in the same direction it takes 75 sec to cross. Find the speed of both the trains.
Solution: It is the case of moving object with length.

Again,
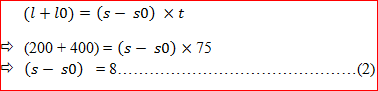
On solving equation (1) and equation (2),
We get: S = 24 m/sec. and SO = 16m/sec.
Solution: Here speed of car = 18 km/hr. = 18 ✖ 5/18 = 5 m/sec.
Since,
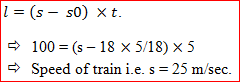

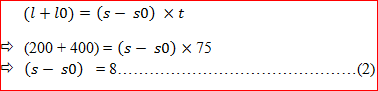
On solving equation (1) and equation (2),
We get: S = 24 m/sec. and SO = 16m/sec.
Question4: A train having length 100 m crosses a car moving in the same direction with a speed of 18 km/hr. in 5 sec. and the same train crosses a platform in 15 sec. Find the length of the platform.
Solution: Here speed of car = 18 km/hr. = 18 ✖ 5/18 = 5 m/sec.
Since,
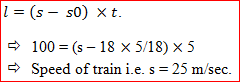
Again,



