
syllogism but In this version of syllogism the, conclusions are given we have to find that to which statement it is being followed. This new version of syllogism has made the applicants panicked , but actually there is no need to get panic, we just have to work on the basics and we will able to solve them, after some practice, you will be able to solve in just few seconds. The basics of solve reverse syllogism are:
syllogism but in this version of syllogism the, conclusions are given we have to find that to which statement it is being followed. This new version of syllogism has made the applicants panicked, but actually, there is no need to get panic, we just have to work on the basics and we will able to solve them, after some practice, you will be able to solve in just few seconds. The basics of solve reverse syllogism are:
The elimination of options
- First, we will try to eliminate the options which are not relating a little bit to statement. This is called elimination process.
- In this process we can take the help of tricks like “ universal negative” if the option is violating this condition should eliminate that option.
- If the sentence is violating the “ particular negative” condition we should also eliminate this.
- If sentence is violating “ universal positive” we should eliminate it.
- If the sentence is violating “ particular positive” condition we should also eliminate the option in this case also. And the last sentence will be your answer.
Let us do with some examples:
Example 1
Conclusions:1. No toxic is injection.
2. Some injections are glucose.
Statements:
Statements:
- All toxic are tablet.
- No tablet is glucose.
- Some glucose are medicine.
- All medicines are injection.
- Some toxic are tablet.
- All tablets are injection.
- Some injection are glucose.
- All glucose are medicine.
- All tablets are toxic.
- No injection is toxic.
- Some glucose are injection .
- All glucose are medicine.
- Some injections are toxic.
- All injections are tablet.
- Some are glucose.
- All glucose are medicine.
- Some medicines are toxic.
- Some toxic are injection some injections are tablet.
- All tablets are glucose.
Solution:
- In this reverse syllogism conclusion 1 disjointed and negative set. So first we will see to find out that option which has the following conclusion statement.
- In option 2,4,5, has no negative statement , so these cannot be the answer.
- In option 1,3 there is negative statement, in option 3 the first and second statement reveals the given conclusion, so the answer is 3.
- As we took two statement 1,3 but I find the relative answer in 3 so I go for that.
Example 2.
Statement: All A are B.
Possible conclusions:
- Some A are B.
- Some B are A.
- Some B are not A.
Here the answer cannot be first and second so third is the answer , which is following the statement.
Example 3.
Statement:- No Rubber is Tank.
- All tanks are bottle.
Possible conclusions:
Solution:
- Some toys are not tank. All cups are bottle. Some rubbers are not tank. All tanks are cup.
- Some rubbers are toy. All rubbers are bottle. Some rubbers are not tank. All tanks are cup.
- Some rubbers are Toy. Some Toys are bottle. Some bottles are tanks. No tank are rubber.
- All rubbers are bottle. All tanks are toys. Some rubbers are toys. All cups are rubber.
- All cups are bottles. No bottle is toy. All rubbers are toys. All tanks are cups.
Solution:
- Statement 2 is universal negative type. So we will have to see that possible conclusion which is followed by this statement. the possible conclusions first and forth are eliminated. And the other options are second , third and fifth are following the statement.
- In second option there is no relativeness means there is no link between bottle and tank so it also should be eliminated.
- So in this way there is fifth option left so this is the answer.
Example 4.
Statement:- All tables are chairs.
- Some beds are not iron.
Possible conclusions:
- All tables are glass.
- Some glasses are beds.
- Some beds are chairs.
- All irons are chairs.
- All tables are glasses.
- All glasses are beds.
- Some tables are not irons.
- All beds are chairs.
- All glasses are tables.
- Some tables are chairs.
- Some beds are injections.
- All beds are irons.
- Some chairs are not tables.
- No chair is glass.
- No table is bed.
- All beds are iron.
- No table is glass.
- All glass are beds.
- All tables are irons.
- All tables are chairs.
Solution:
- In this statement there is no universal negative statement. now we can go through the particular negative statement.
- In first and second statement there is no negative violation, so these options should be eliminated.
- In forth statement there is no meaning of that i.e. All beds are irons. So it cannot be answer.
- So we are left with fifth and second option , but in fifth option it is already giving the first conclusion and there is no restrictions on iron and bed. So it also cannot be the answer.
- So the only one option left which is second option , this is the answer.
Example 5.
Statement: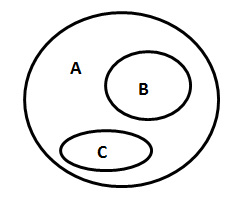
All B is A and All C is A.
Possible conclusions :
Between B and A Between C and A
All B is A All c is A
Some B is A Some C is A
Some A is B Some A is C
- Here we find that there is no relativeness in B and C . So there is no possiblity to have any conclusion from B and C.
- There is no DIRECT CONNECTION between B and C. So it is not possible to derive any conclusion between B and C.
- So these were some tricks to solve the reverse syllogism , which helps the applicants to solve the reverse syllogism, these tricks helps them to understand the trick in just a few seconds and make it easy for them , so reverse syllogism is no more the tough one to solve in all competitive exams, because in all competitive exams syllogism is one of the important topics.

