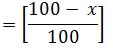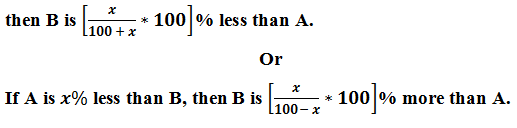Percentage is a fraction whose denominator is always 100. x percentage is represented by x%.

Example: - If 10% of A is equal to 12% of B, then 15% of A is equal to what percent of B?
Example: - If income of Ravi is 20% more than that of Ram, then the income of Ram is how much percent less than that of Ravi?
Example: - Pankaj Sharma has to score 40% marks to get through. If he gets 40 marks and fails by 40, then find the total marks set for the examination?
Example: - Raj scores 30% and fails by 60 marks, while Rohan who scores 55% marks, gets 40 marks more than the minimum required marks to pass the examination. Find the maximum marks for the examination?

Example: - Ram can buy 5 Kg more sugar in rupees 100 as the price of sugar has decreased by 10%. Find the actual price of the sugar?

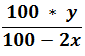 Example: - In an election contested by two candidates, one candidate got 40% of total votes and still lost by 500 votes, find the total number of votes casted?
Example: - In an election contested by two candidates, one candidate got 40% of total votes and still lost by 500 votes, find the total number of votes casted?
I. Population after ‘n’ years :

II. Population ‘n’ years ago :

Example: - The population of a town is 352800. If it increases at the rate of 5% per annum, then what will be its population after 2 years and 2 years ago?
Example: -The salary of a worker is first increased by 5% and then it is decreased by 5%. What is the change in his salary?
Calculation of Percentage
If we have to find y% of x, then
1. To express x% as a fraction :
We know
x% = x/100
Thus 10% = 10/100 (means 10 parts out of 100 parts)
= 1/10 (means 1 part out of 10 parts)
2. To express x/y as a percentage :
We know that x/y = (x/y× 100 )
Thus 1/4 = ( 1/4 ×100 )% = 25%
and 0.8 = ( 8/10 ×100 )% = 80%


3. To increase a number by a given percentage(x%):
Multiply the number by the following factor
4. To decrease a number by a given percentage(x%):
Multiply the number by the following factor5. To find the % increase of a number:
6. To find the % decrease of a number:

Some Observation
#1
If 20% candidate failed in an exam then observations are- 80% represent passed in exam
- 100% represent total appeared in exam
- (80%-20%) = 60% represent difference between passed and failed candidate in exam
#2
If a number is increased by 25% then observations are
- 100% represent the old number
- 125% represent the new number.
#3
Remember that Base in the given sentence (Question) is always 100%
Eg. Income of Ram is increased by 20%
In this sentence
100% - represent the income of Ram
20% - represent increment
120% - represent new income of Ram.
Remember it :
1 = 100%
1/2 = 50%
1/3 = 33 1/3%
1/4 = 25%
1/5 = 20%
1/6 = 162/3%
1/7 = 142/7%
1/8 = 121/2%
1/9 = 111/3%
1/10 = 10%
1/11 = 91/11%
1/10 = 81/3%
1/13% = 79/13%
25% = 1/4
6.25% = 1/16
125% = 5/4
150% = 3/2
200% = 2
350% = 7/2
#4
If of A is equal to y% of B then -Example: - If 10% of A is equal to 12% of B, then 15% of A is equal to what percent of B?
#5
If A is more than B,Example: - If income of Ravi is 20% more than that of Ram, then the income of Ram is how much percent less than that of Ravi?
#6
If the passing marks in an examination is P%. If a candidate scores S marks and fails by F marks then–Example: - Pankaj Sharma has to score 40% marks to get through. If he gets 40 marks and fails by 40, then find the total marks set for the examination?
#7
If a candidate scores marks and fails by a marks while an another candidate scores y% marks and gets b marks more than minimum passing marks, then –Example: - Raj scores 30% and fails by 60 marks, while Rohan who scores 55% marks, gets 40 marks more than the minimum required marks to pass the examination. Find the maximum marks for the examination?

#8
If due to decrement in the price of an item, a person can buy Kg more in y rupees, then actual price of that item -Example: - Ram can buy 5 Kg more sugar in rupees 100 as the price of sugar has decreased by 10%. Find the actual price of the sugar?

#9
If in an election, a candidate got of total votes cast and still lose by y votes, the total number of votes cast –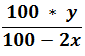
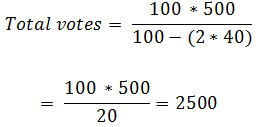
#10
If the population of a town is P and it increases or decreases at the rate of R% per annum then –I. Population after ‘n’ years :

II. Population ‘n’ years ago :

Example: - The population of a town is 352800. If it increases at the rate of 5% per annum, then what will be its population after 2 years and 2 years ago?
#11
If the value of a number is first increased by and again decreased by the net effect is always decreased by x2/100%Example: -The salary of a worker is first increased by 5% and then it is decreased by 5%. What is the change in his salary?
Examples
#1
Q. If the difference between 62% of a number and 3/5th of that number is 36. what is the number ?
Sol:
Let the number be x.
Then x × 62% - x × 3/5 = 36
x ×62% -x V 60% = 36 (60% = 3/5)
x ×2% = 36
x ×2/100 =36
x = 36 ×100/2 = 1800
#2
Q. 40% of Ram's income Rs. 1200 Then Find
- 75% of Ram's income ?
- 1/4 part of Ram's income ?
- 1/3 part of Ram's income ?
(1)
40% = 1200 Rs.
75% = 1200/40 ×75 = 2250 Rs.
Trick : 1200 / 40 × 75 = Rs. 2250/-
(2)
40% of income = Rs. 1200
Then 1/4 part (i.e. 25% ) of Ram's
income = 1200/40 ×25
= Rs. 750/- Ans
(3)
40% of Ram's income
= Rs. 1200
i.e. 2/5 part of Ram's income
= Rs. 1200
Then total income of Ram
= Rs. 1200 ×5/2
1/3 part of Ram's income
= Rs. 1200 × 5/2 × 1/3
= Rs. 1000 Ans.
Trick :
1200/2/5 × 1/3
= 1200/2 × 5/3 = 1000