Geometry Basics - Circles Theorems

Geometry is a trending topic in Bank exams. In the series of sharing Geometry basics, today I am sharing rules related to Circles :-

Area of the circle is A=πr²

Circumference (perimeter) of the circle= 2πr

Sector of a Circle

To find the area of the sector we must know the central angle .Suppose the central angle is θ.

Chords of a Circle

The longest chord in a circle is diameter.

AB, CD, EF are the different chords of the circle. You can see that as you move away from the centre the length of the chord gets smaller and smaller but as you move towards the centre, the length of the chord becomes greater and greater.

Based on the same logic , there can be many questions like :

Q1.

The two parallel chord of a circle are 10 and 12 cm and the radius of the circle is 13 cm. Find the distance between two chords .

Solution : In this question there can be two possibilities about the locations of the chords .

Both the chords are on the opposite side of the center.
Both the chords are on the same side of the center.

Let us solve it with first possibility

Here one theorem comes into existence that says that any perpendicular drawn from the center of the circle to chord, divides the chord.

Since OP is a perpendicular on the chord AB

Therefore AP=PB =12

In triangle OPB by Pythagorean Theorem

OP² = OB² –PB²

= 13²-12²

= 169-144

= 25

OP= 5 cm

Similarly since OR is perpendicular to the chord AB

Therefore CR=RD =5 cm

In triangle ORD by Pythagorean theorem

OR² = OD²-RD²

= 13²-5²

= 169-25

=144

OR = 12

Therefore the distance between the chords AB and CD = OP+OR =5+12=17 cm

Now let us do it with second possibility

In this case also OP and OR will remain 5 cm and 12 cm respectively.

We need to find out the PR

PR = OR –OP = 12-5 = 7 cm

Therefore the distance between the two chords = 7 cm

Angles in a circle

Angles in the major segement

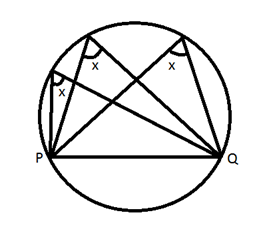
RULE 1:

According rule the angles made in the same segments are equal.

Angles made by the same chord in the same segment are always equal.

Remember that there can be any number of angles but if they are

in the same segment, they are always equal.

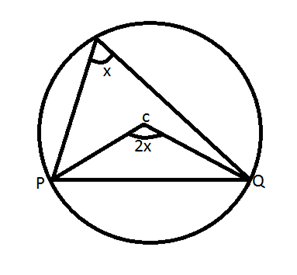
RULE 2:

Angles made by the chord at center are twice the angle made at the circumference.

Angles in the minor segment