Geometry Theorems - Triangles

Important Geometry theorems

Must read - Important Axioms and Theorems: Transversal and Parallel lines 

Theorem 3  : Angle sum property of a triangle.

The sum of the angles of a triangle is 180⁰.

In the picture above, PQR is a triangle with angles 1, 2 and 3

Then according to the theorem

Angle 1+Angle 2 +Angle 3 =180⁰

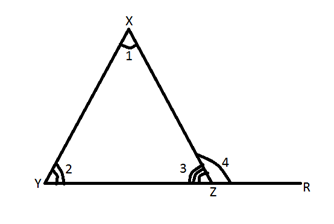
Theorem 4

If a side of a triangle is produced then the exterior angle so 

formed is equal to the sum of two interior opposite angles.

In the picture above XYZ is a triangle whose side YZ is extended 

to R. 1, 2, and 3 are the interior angles of a triangle. Angle 1 and 

Angle 2 are the interior angles opposite to the exterior angle 4

Then according to the theorem

Angle 4 = Angle 1+ Angle 2

Let us do some questions based on these theorems.

Ques. - In the figure  if QT is perpendicular PR , Angle TQR = 40⁰  and Angle SPR =30⁰, find x and y .

Solution : In triangle QTR

Angle TQR +Angle QRT +Angle QTR =180⁰

40⁰ + y + 90⁰ =180⁰

  y =180⁰-130⁰

     = 50⁰

Angle QSP = Angle SPR +Angle SRP

Reason:Exterior angle = sum of interior opposite angles

  x = 30⁰ +y

  x = 30⁰ +50⁰

  x =80⁰

Ques. - In the figure below XY II MN , Angle YXZ  =350  and angle ZMN =530, find angle MZN.

Solution:

We know that XY is parallel to MN.

Angle MNZ = Angle ZXY  ( alternate interior angles)

                      = 35⁰

Now in triangle MZN

Angle ZMN +Angle MNZ +Angle MZN =180⁰

53⁰ +35⁰ +Angle MZN =180⁰

Angle MZN = 180⁰-88⁰

Angle =92⁰

Ques - In the figure given below  If PQ and RS intersect at T, such that angle PRT =40⁰, angle RPT=95⁰ and angle TSQ=75⁰, find SQT.

Solution:

In triangle PRT

40⁰+95⁰+Angle RTP =180⁰

 Angle RTP =180⁰-135⁰

Angle RTP =45⁰

Angle STQ =Angle RTP ( vertically Opposite angle )

                    =45⁰

Again in triangle TQS

Angle STQ + Angle SQT + Angle TSQ = 180⁰ ( Angle sum property)

45⁰+ Angle SQT +75⁰ =180⁰

Angle SQT =180⁰-120⁰

Angle SQT = 60⁰

Ques. In the figure if PQ is perpendicular to PS, PQ II SR Angle SQR =28⁰  and Angle QRT =65⁰, then find the values of x and y .

Solution:

Since PQ II SR

Angle QRT = Angle PQR (alternate interior angles )

65⁰ = x +28⁰

 X= 65⁰-28⁰

    = 37⁰

In triangle PQS

Angle PSQ +Angle PQS + QPS = 180⁰ ( angle sum property)

 Y +x +90⁰ =180⁰

 Y+37⁰+90⁰=180⁰

Y =180⁰-127⁰

   = 53⁰