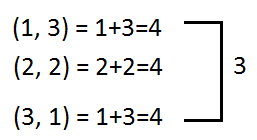Today I am going to share basic concepts for Dice problems from Probability.
(1, 1) = 1+1=2
If 1 appears on the first dice and 2 on the second dice, the sum = 3
(1, 2) = 1+2=3
If 1 appears on the first dice and 3 on the second dice, the sum = 4
(1, 3) = 1+3=4
If 1 appears on the first dice and 4 on the second dice, the sum = 5
(1, 4) = 1+4=5
If 1 appears on the first dice and 5 on the second dice, the sum = 6
(1, 5) = 1+5=6
If 1 appears on the first dice and 6 on the second dice, the sum = 7
(1, 6) = 1+6=7
After that dice will repeat like:
(2, 1) = 2+1=3
(2, 2) = 2+2=4
(2, 3) = 2+3=5
(2, 4) = 2+4=6
(2, 5) = 2+5=7
(2, 6) = 2+6=8
Then gain
(3, 1) = 3+1=4
………….
………….
………….
(3, 6) = 3+6=9
Similarly if
(6, 1) = 6+1=7
……….
………..
And so on
(6, 6) = 6+6=12 (Maximum)
Now if two dices are rolled together
Minimum sum =2
Maximum sum = 12
Now if the question says
The sum of 6 can be obtained by:
Types
- Cards
- Balls
- Coins
- Dice
If two dices are thrown: Sum of dices
If 1 appears on the first dice and 1 on the second dice, the sum = 2 (Minimum sum)(1, 1) = 1+1=2
If 1 appears on the first dice and 2 on the second dice, the sum = 3
(1, 2) = 1+2=3
If 1 appears on the first dice and 3 on the second dice, the sum = 4
(1, 3) = 1+3=4
If 1 appears on the first dice and 4 on the second dice, the sum = 5
(1, 4) = 1+4=5
If 1 appears on the first dice and 5 on the second dice, the sum = 6
(1, 5) = 1+5=6
If 1 appears on the first dice and 6 on the second dice, the sum = 7
(1, 6) = 1+6=7
After that dice will repeat like:
(2, 1) = 2+1=3
(2, 2) = 2+2=4
(2, 3) = 2+3=5
(2, 4) = 2+4=6
(2, 5) = 2+5=7
(2, 6) = 2+6=8
Then gain
(3, 1) = 3+1=4
………….
………….
………….
(3, 6) = 3+6=9
Similarly if
(6, 1) = 6+1=7
……….
………..
And so on
(6, 6) = 6+6=12 (Maximum)
Now if two dices are rolled together
Minimum sum =2
Maximum sum = 12
Now if the question says
What is the probability of getting a sum of 4 if two dices are rolled together?
We can see that the sum of 4 can be obtained by:
Solution: Total out comes = 6*6=36 (because two dices are thrown so the total outcome will be 36)
The required probability = Favorable outcomes /Total outcomes = 3/36=1/12
The required probability = Favorable outcomes /Total outcomes = 3/36=1/12
What is the probability of getting a sum of 6 if two dices are thrown?
Solution:The sum of 6 can be obtained by:
So the probability = 5/36
Now to find out the probability of a sum when two dices are thrown, there is a shortcut which is based on the diagram below.
Note: Memorize this picture to solve probability sums
Sum 4: Probability 3
Sum 12: Probability 1
So the required probability = 3/36+1/36 =4/36=1/9.
Read more about Probability here
Now to find out the probability of a sum when two dices are thrown, there is a shortcut which is based on the diagram below.
Let us solve some problems
So the required probability = 4/36= 1/9.
So the required probability is 3/36 that is 1/12.
Solution: From the picture
Sum 6: probability 5
Sum 11: probability 2
The required probability = 5/36+2/36= 7/36
What is the probability of getting a sum of 5 if two dices are thrown together?
Solution: Observe the picture very carefully we can see if the sum is 5, the probability is 4.So the required probability = 4/36= 1/9.
What is the probability of getting a sum of 10 if two dices are thrown together?
From the picture if the sum is 10, the probability is 3.So the required probability is 3/36 that is 1/12.
What is the probability of getting a sum of 6 or 11 if two dices are rolled together?
Sum 6: probability 5
Sum 11: probability 2
The required probability = 5/36+2/36= 7/36
What is the probability of getting a sum of 4 or 12 if two dices are rolled together?
Solution: From the pictureSum 4: Probability 3
Sum 12: Probability 1
So the required probability = 3/36+1/36 =4/36=1/9.
Read more about Probability here