
Meaning and Introduction
The word "Percent" means hundred. For example 25% means, 25 parts out of 100 parts and this can be written as 25/100.
We can also say that, percent is a fraction whose denominator is 100 and the numerator is known as 'Rate Percent'. 25/100 = 25 percent. Here, 25 percent is the rate.
Table given below helps you to understand the some basic fractions and its percentages. This table is helpful for you to solve the percentages questions quickly.

Conversion of Fraction to Rate Percent
We can understand this point with example.
Q. Express 4/5 in rate percent.
Ans. 4/5 × 100 = 80%
Conversion of Rate Percent to Fraction
Example - 9% can be converted to a fraction as 9/100 = 0.09
Rate Percent of a Number
Here is the formula to find out the rate percent of a number i.e.

Ans. 500 × 75/100 = 375
Some Simple Questions based on Percentages
Example - 5% of what number is 35?
Ans. 5% × X = 35
X = 35/5 × 100
X = 700
That means 5% of 700 is 35.
Example - If 30% of a number is 48, then what is 70% of the number and also find the 100% of a number?
Ans. Here, unitary method can be used to save the time
30% of a number is = 48
1% of a number is = 48/30
70% of a number is = 48/30 × 70
= 112Now, we have to find the 100% of a number
70% of a number is = 112
1% of a number is = 112/70
100% of a number is = 112/70 × 100
= 160
Example - If 40% of the number exceeds the 25% of it by 54. Find out the number.
Ans. Now, 54 is the difference as given in the question. To find the number of these types of questions, following formula is used.

Expressing a Given Quantity as a Percentage of Another Given Quantity
x is what % of y?
The question simply indicates that on the basis of 'y' find out the % of 'x' hence 'y' is the basis of comparison so, 'y' will be the denominator.
Formula is:
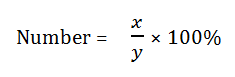
Example - 45 is what percent of 900 or what percentage of 900 is 45?
Ans. Using the above concept, we find here that 900 is the basis of comparison and hence 900 will be the denominator.
The required percentage = 45/900 × 100%
= 5%
= 5%
Percentage Change
This % increase or % decrease has wide application in solving the problems on Data Interpretation. It helps you to solve the problems of Data Interpretation as well as Percentage chapters. Following formula is applied if a number or quantity increases or decreases to a new number.
Example - A person invested 32,000 and Rs. 40,000 respectively in 2010 and 2011. What is the percentage increase in year 2011 from the previous year.
Ans. Required % increase =

Percentage Change and New Number
If any number (quantity) is increased by x%, then following formula should be keep in mind.
Similarly, if any number (quantity) is deceased by x%, then
Note - In case of percentage decrease, a (-)ve sign is put before x, otherwise the formula is same).
Example - The present salary of Anuj is Rs. 5000. This will be increased by 20% in the next year. What will be the increased salary of Anuj?
Ans. As given in the question, the salary is to be increased by 20%.
20% is equivalent to 0.20 or 1/5
So, now we can apply the formula like:
The increased salary = 5000 (1+ 0.2)
= 5000 × 1.2
= 6000
or
or
The increased salary = 5000 × (100 +20) / 100
= Rs. 6000
Two Step Change of Percentage For A Number
If a number is changed (increased or decreased) by x% and in the second step, this changed number is again changed (increased or decreased) by y% then net percentage change on the original number can be conveniently found out by using the following formula,

Example - If a number is increased by 12% and then decreased by 16%, then find the net percentage change in the number.
Ans. We will apply the formula as shown under:
Net % change = x + y + (xy)/100
Let x = 12 and y = - 16
Net % change = 12 + (-16) + [12 × (-16)] / 100
= 12 - 16 + [-1.92]
= - 4 - 1.92
= - 5.92
(-) sign signifies that there is percentage decrease in the result. Therefore - 5.92 indicates net 5.92% decrease of the given number as a result of 12% increase and 16% decrease.
(It also implies that 12% increase and 16% decrease are equivalent to 5.92% decrease)
% Excess or % Shortness
Sometimes, we meets with questions like If a number A is x% more than a number B, then B is y% less than A. This % more (excess) or % (shortness) can be calculated by using the following formula

Example - If income of Akram is 20% less than Bashir, then find out how much percent Bashir's income is more than Akram?
Ans. As we read earlier that 'y' is used for less that means y = 20 and we have to find out 'x' by applying formula as shown below:
(1/20) - (1/x) = 1/100

So, Above are some formulas to understand the "Percentage" chapter. So, keep the practice and All The Best.
==>> Follow Quantitative Aptitude series



