Application of LCM and HCF

Application of LCM and HCF :-

Problems

Question 1. What is the greatest number that will divide 2930 and 3250 and will leave as remainders 7 and 11 respectively?

Solution:  The greatest number will be the HCF of (2930 – 7) and (3250 – 11),  i.e. 79.

Question 2. What is the least number by which 825 must be multiplied in order to produce a multiple of 715?

Solution: 825 = 3 × 5 × 5 ×11;                  715 = 5 × 11 × 13

Any multiple of 715 must have factors of 5, 11 and 13. So, 825 should be multiplied by the factor(s) of 715, which is (are) not present in 825. 

∴ The required least number = 13

Question 3. The LCM of two numbers is 2310 and their HCF is 30. If one of the numbers is 7 × 30, find the other number.

Solution: the required number = (2310 ×30)/(7 ×30) = 330.

Question 4. Three bells commence tolling together and they toll after 0.25, 0.1 and 0.125 seconds. After what interval will they again toll together? 

Solution: They will toll together after an interval of time equal to the LCM of  0.25 sec, 0.1 sec and 0.125 sec.

LCM of 0.25, 0.1 and 0.125 = (LCM of 250, 100 and 125) × 0.001

                                      = 500 × 0.001 = 0.5 sec.

Question 5. What is the smallest sum of money which contains Rs. 2.50, Rs. 20, Rs. 1.20 and Rs. 7.50? 

Solution: LCM of 2.5, 20, 1.2 and 7.5 = (LCM of 25, 200, 12 and 75) 

Here the highest number of decimal is 1 so we multiply each by 10 to get 25, 200, 12 and 75.

Their LCM is  = 600 but since we multiplied by 10 so bring back the original value we need to divide it by 10

so the required solution = 600/10= 60

Question 6. What is the greatest number which will divide 410, 751 and 1030 so as to leave the remainder 7 in each case?

Solution: the required number will be the HCF of (410-7), (751 – 7), (1030 – 7)  i.e. 31.

Question 7. What is the HCF of 4/5 , 5/6 and 7/15 ?

Question 8. Three men start together to travel the same way around a circular track of 11 km. Their speeds are 4, 5.5 and 8 km per hour respectively. When will they meet at the starting point?

Question 9. How many times is the HCF of 48, 36, 72 and 24 contained in their LCM?Solution: HCF of 48, 36, 72, 24 = 12;                
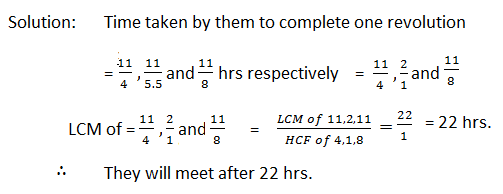
                LCM of 48, 36, 72, 24 = 144

∴ LCM = 12 × HCF. (12x12 =144)

Question 10. Find the least square number which is exactly divisible by 4, 5, 6, 15 and 18.Solution: LCM of 4, 5, 6, 15 and 18 = 180, which is exactly divisible by the given numbers.

180 = 2 × 2 × 3 × 3 × 5 

You can see that 2 and 3 are paired but 5 is not . To make it paired we need to multiply by 5 so that the whole multiplication becomes a perfect square.

Therefore, if 180 is multiplied by 5 (180 × 5 = 900) and 900 will be a perfect square as well as divisible by 4, 5, 6, 15 and 18.

Question 11. Find the sum of a numbers between 300 and 400 such that when they are divided by 6, 9 and 12. 

(i) it leaves no remainder;   and

(ii) it leaves remainder as 4 in each case.

Solution: The LCM of 6, 9, and 12 = 36

(i) Multiples of 36 which lie between 300 and 400 are 324,                  

 360 and 396.

∴  The required least number = 324 + 360 + 396 = 1080

(ii) Here the remainder is 4 in each case

So, the numbers are (324 + 4) = 328 and (360 + 4) = 364. (The number 396 + 4 = 400 does not lie between 300 and 400 so it is not acceptable.) 

∴    The required sum = 328 + 364 = 692.