LCM (Least Common Multiple) - Concept and Questions with Answers

COMMON MULTIPLE: A common multiple of two or more numbers is a number which is exactly divisible by each of them.

Least common multiple (LCM): The LCM of two or more given numbers is the least number which exactly divisible by each of them.

Thus, 15 is a common multiple of 3 and 5.

30 is a common multiple of 3 and 5.

45 is a common multiple of 3 and 5.

But 15 is the least common multiple (LCM) of 3 and 5.

To find the LCM of two or more given numbers

Method I: Method of Prime Factors

Rule: Resolve the given numbers into their prime factors and then find the product of the highest power of all the factors that occur in the given numbers. The product will be the LCM.

Example: Find the LCM of 8, 12, 15 and 21.

Solution:                8 = 2 x 2 x 2 =2²

                             12 = 2 x 2 x 3 = 2² x 3

                             15 = 3 x 5

                             21 = 3 x 7

Here, the prime factors that occur in the given numbers are 2, 3, 5 and 7 and their highest powers are respectively 2², 3, 5 and 7.

Hence, the required LCM = 2² x 3 x 5 x 7 = 840

Method II : Division Method

To find Least Common Multiple by using Division Method we need to follow the following steps.

Step 1: Write the given numbers in a horizontal line, separating them by commas. 

Step 2: Divide them by a suitable prime number, which exactly divides at least two of the given numbers.

Step 3: We put the quotient directly under the numbers in the next row. If the number is not divided exactly, we bring it down in the next row.

Step 4: We continue the process of step 2 and step 3 until all co-prime numbers are left in the last row.

Step 5: We multiply all the prime numbers by which we have divided and the co-prime numbers left in the last row. This product is the least common multiple of the given numbers.

1. Find least common multiple (L.C.M) of 20 and 30 by division method. 

Solution:

LCM = 2 x 2 x 5 x 3 =60

LCM OF DECIMALS

Rule : Fist make (if necessary) the same number of decimal places in all the given numbers; then find their LCM as if they were integers, and mark in the result as many decimal places as there are in each of the numbers.

Example: Find the LCM of 0.6, 0.9 and 0.36.

Solution:    The given numbers are equivalent to 0.60, 9.60 and 0.36.

Now, find the LCM of 60, 960 and 36.Which is equal to 2880.

Therefore, the required LCM = 28.80.

LCM OF FRACTIONS

The LCM of two or more fractions is the least fraction or integer which is exactly divisible by each of them.

Questions based on LCM

• The LCM of two numbers is 2079 and their HCF is 27. If one of the numbers is 189, find the other.

Solution:   

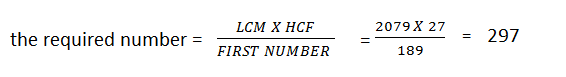
• Which is the least number which, when divided by 52, leaves 33 as a remainder, and when divided by 78 leaves 59, and when divided by 117 leaves as 98 as the respective remainders?

Solution:   

         Since 52 – 33 = 19, 78 – 59 = 19, 119 – 98 = 19

We see that the remainder in each case is less than the divisor by 19. Hence, if 19 is added to the required number, it becomes exactly divisible by 52, 78, and 117. Therefore, the required number is 19 less than the LCM of 52, 78, and 117.

The LCM of 52, 78 and 117 = 449

Therefore, the required number = 468 – 19 = 449

• Find the greatest number of six digits which, on being divided by 6, 7, 8, 9 and 10, leaves 4, 5, 6, 7 and 8 remainders respectively.

Solution:           

         The LCM of 6, 7, 8, 9 and 10 = 2520

          The greatest number of six digits = 999999

Dividing 999999 by 2520, we get 2079 as remainder. Hence the 6-digit number divisible by 2520 is (999999 – 2079), or 997920.

Since 6 – 4 = 2, 7 – 5 = 2, 8 – 6 = 2, 9 – 7 = 2, 10 – 8 = 2, the remainder in each case is less than the divisor by 2.

Therefore, the required number = 997920 – 2 = 997918

• What least number must be subtracted from 1936 so that the remainder when divided by 9, 10, and 15 will leave in each case the same remainder 7?

Solution:      

                    The LCM of 9, 10 and 15 = 90

On dividing 1936 by 90, the remainder = 46

But 7 is also a part of this remainder

Therefore, the required number = 46 – 7 = 39

• What greatest number can be subtracted from 10,000 so that the remainder may be divisible by 32, 36, 48 and 54?

Solution:         

         The LCM of 32, 36, 48 and 54 = 864

Therefore, the required greatest number  = 10,000 – 864 = 9,136