
Question 1:
Walking at a speed 20% less than that of usual speed a person reaches his office 15 minutes late. Find the usual time and new time required for reaching office.
Walking at a speed 20% less than that of usual speed a person reaches his office 15 minutes late. Find the usual time and new time required for reaching office.
Solution: We will solve this question by 2 methods:
Basic Concept: Let usual speed be ‘s’ and usual time taken is ‘t’. Then new speed is ‘0.8s’ and new time taken is (t + 15).
Note: In this question the unit of any parameter is not required.
Since, the distance is constant. We can apply the basic formula, distance = speed ✖ time.
i.e. S1 ✖ T1 = S2 ✖ T2.
➔ s ✖ t = 0.8s ✖ (t+15)
➔ 0.2t = 12
➔ t = 60 minutes.
➔ So, new time taken = (60+15) minutes = 75 minutes.
Shortcut method:
By taking ratio of usual and new speed i.e. s:0.8s = 5:4

➔ 5x – 4x = 15
➔ x = 15.
So usual time taken = 4x = 60 minutes and new time taken = (60+15) = 75 minutes.
Question 2:
A person covered certain distance from his home to park at a speed of 20km/hr. and reached 10 minutes late, had he travelled the same distance with a speed of 30km/hr. he would have reached 20 minutes earlier. Find the distance between home and mall and the speed at which he should travel to reach on time.
A person covered certain distance from his home to park at a speed of 20km/hr. and reached 10 minutes late, had he travelled the same distance with a speed of 30km/hr. he would have reached 20 minutes earlier. Find the distance between home and mall and the speed at which he should travel to reach on time.
Solution: Let the normal time taken be ‘t’. Since distance = speed ✖ time.
➔ S1 ✖ T1 = S2 ✖ T2
➔ 20 ✖ (t+10) = 30 ✖ (t-20)
➔ 10t = 800. So, t = 80minutes.
So, time taken with speed 20km/hr. is 90 minutes and with speed 30 km/hr. is 60 minutes.
Now, Distance between Home and mall = 20 ✖ 90/60 = 30 ✖ 60/60 = 30km.
Concept 4:

This formula only satisfies when the distance travelled in each case with different speed u, v, w, x are same. If distances travelled are different then we will solve it with the basic formula as: 
Let a car goes from ‘A’ to ‘B’ with speed ‘u’ km/hr. and then it goes from ‘B’ to ‘C’ with speed ‘v’ km/hr. Then find the average speed.
Let the distance between ‘AB’ be ‘x’ and distance between ‘BC’ is ‘y’. Then:

Question 3:
Salman went from Delhi to Jaipur with the speed of 60km/hr. and return back with the speed of 90km/hr. Find the average speed.
Salman went from Delhi to Jaipur with the speed of 60km/hr. and return back with the speed of 90km/hr. Find the average speed.
Solution: We can directly apply the formula here i.e.

Question 4:
Ram covered 4 rounds of a circular track with different speeds of 10km/hr, 20 km/hr, 30 km/hr, 40 km/hr. respectively. Find the average speed of the whole journey.
Ram covered 4 rounds of a circular track with different speeds of 10km/hr, 20 km/hr, 30 km/hr, 40 km/hr. respectively. Find the average speed of the whole journey.
Solution:

Question 5:
A person goes from A to B i.e. 60 km and from B to C i.e. 80 km with the speed of 20km/hr. and 10km/hr. respectively. Find his average speed in the whole journey.
A person goes from A to B i.e. 60 km and from B to C i.e. 80 km with the speed of 20km/hr. and 10km/hr. respectively. Find his average speed in the whole journey.
Solution:

Question 6:
The speed of a train is 54 km/hr. without stoppage and 45 km/hr. with stoppage. Find for how much time in an hour the train stops.
The speed of a train is 54 km/hr. without stoppage and 45 km/hr. with stoppage. Find for how much time in an hour the train stops.
Solution:
Distance travelled by train in 1 hour without stoppage = 54 km.
Distance travelled by train in 1 hour with stoppage = 45 km.
If we see here closely then we observe:
54 km distance is travelled in 60 minutes. If the train will travel 45 km without stoppage then
time taken by it is

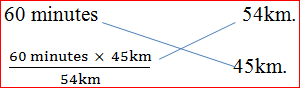

So, for (60 – 50) minutes = 10 minutes the train stops.
Shortcut:

= 50 minutes. So, stoppage time = (60 – 50) = 10 minutes.


