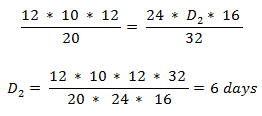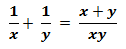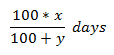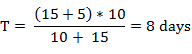Work
Amount of job assigned or the amount of job actually done.
Note: Work done is always considered to be equal to 1.
Time and Work - Shortcuts and Tricks
Example: - 12 persons can make 20 toys in 10 days working 12 hours a day. Then in how many days can 24 persons make 32 toys working 16 hours a day?
Time taken by (A + B) to complete the work –
If ‘n’ persons (more than two) are there then their one day’s work =
Where x1,x2, x3 …………… represents the number of days taken by them to complete the work.
Example: - If A can do a piece of work in days and B can do the same work in days. If both are working together, how many days will they take to complete the work?
(A + B)’s one day work =
(A + B) will complete the whole work =
Example: - A & B together can do a piece of work in days and A alone can do it in 18 days. In how many days can B alone do it?
Example: - A & B can do a piece of work in days, B & C can the same work in 9 days and A & C can do it in days, then find the time in which A, B & C can finish the work if they working together?
Example: - Komal can do a work in days and Pooja is more efficient than Komal to complete the same work, then find the total time taken to complete the work by Pooja?
Example: - If A alone does a piece of work, he takes days more than the time taken by (A + B) to do complete the work, while B alone takes 9 days more than the time taken by (A + B) to finish the work. What time A & B together will take to finish the work?
I. A leaves the work ’n’ days before its completion, then total time taken for completion of work :
II. B leaves the work ’n’ days before its completion, then total time taken for completion of work :
Example: - A can do a piece of work in days while B can do it in days. They begin together but 5 days before the completion of the work, B leaves off. Find the total number of days for the work to be completed?
Relations between work, time and person: -
- Work & Person: Directly proportional i.e. more work, more person required.
- Time & Person: Inversely proportional i.e. more people, less time required.
- Work & time: Directly proportional i.e. more work, more time required.
Note: Work done is always considered to be equal to 1.
Rules: -
- If a person can do a piece of work in ‘n’ days/ hours then that person’s one day’s/ hour’s work = 1/n
- If a person’s one day’s/ hour’s work = 1/n , then he will complete then he will complete the work in ‘n’ days/ hours.
- If first person is ‘n’ times efficient than second person then work done by first person : second person = n : 1
- If the ratio of number of men required to complete a work is m : n then the ratio of time taken by them will be n : m.
Formulas Including Short Tricks:
# 1.
If persons can do W1 work in D1 days working T1 hours in a day and M2 Persons can do W2 work in D2 days working T2 hours in a day then the relationship between them is
# 2.
If A can do a piece of work in days and B can do the same work in days then (A + B)’s one day work-
Example: - If A can do a piece of work in days and B can do the same work in days. If both are working together, how many days will they take to complete the work?
(A + B)’s one day work =
# 3.
If A & B can complete a work in days and A alone can finish that work in days then number of days required by B to complete the work–
# 4.
If A & B can do a piece of work in days, B & C can the same work in days and A & C can do it in days, then working together A,B & C can do that work in–
# 5.
If A can do a work in days and B can do faster than A, then B will complete the work in -
# 6.
If A takes days more to complete a work than the time taken by (A + B) to do the same work and B takes y days more than the time taken by (A + B) to do the same work then (A + B) do the work in √xy days –Example: - If A alone does a piece of work, he takes days more than the time taken by (A + B) to do complete the work, while B alone takes 9 days more than the time taken by (A + B) to finish the work. What time A & B together will take to finish the work?
# 7.
If A & B each alone can do a piece of work in days respectively. Both begin together but –I. A leaves the work ’n’ days before its completion, then total time taken for completion of work :
# 8.
If A & B do a piece of work in days respectively. Both begin together but after some days, A leaves off & the remaining work is completed by B in ‘n’ days. Then the time after which A left, is given by 
Example: - A & B do a piece of work in days respectively. Both begin together but after a certain time, A leaves off. In this case, B finishes the remaining work in 20 days. After how many days did A leave?
