Today I am going to summarise all the maths tricks that will speed up your calculation speed. I used them for CAT and IBPS exams. I am sure that these tricks will help you increase your score. I have written many articles in detail on these topics. Click on respective links to get details.
Squaring
In this simple trick, we need to modify the equation and make the units digit zero. After all, it is easy to multiply when units digit is zero.
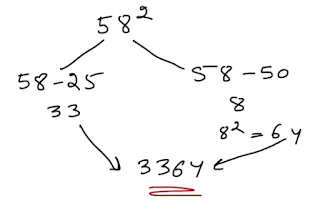
For example - Find square of 43
= (43+3) × (43-3) + (3×3)For example - Find square of 43
=(46×40) + 9
= (460×4) + 9
= 1840 + 9 = 1849
Finding Square of Any No. From 1 to 100
Read my full post on Squaring trick,
Multiplication
Vedic maths gave us the easiest method to do complex multiplications quickly. This method can be quickly explained with an example.Multiply 62 with 32
Step 1
Step 2
Step 3
Detailed post on Multiplication technique (Multiplication of 3 digit numbers)
Read quick Multiplication technique without using complicated Vedic maths
For example 99×5= 990/2= 495
Step 3
Detailed post on Multiplication technique (Multiplication of 3 digit numbers)
Read quick Multiplication technique without using complicated Vedic maths
Multiplication with 5
Simply multiply the number by 10 and then divide it by 2.For example 99×5= 990/2= 495
Multiplication with 99
Multiply the number with 100 and then minus the same number from the result. Let's take an exampleMultiply 32×99 = 3200 - 32 = 3168
Mixture
Questions related to mixtures can be easily solved by alligation method. By using alligation we can wide arrange of maths questions. Let me explain this with a simple example
Example
The price of wine of $60 per litre. If Samuel is adding water with and selling the mixture for $40 per litre. Profit margin remains same. What is the ratio of water and wine in the mixture?
Detailed post on Alligation method (Application on various types of questions)
Example
The price of wine of $60 per litre. If Samuel is adding water with and selling the mixture for $40 per litre. Profit margin remains same. What is the ratio of water and wine in the mixture?
Square Root:
Square root of 4096:
Here the one's digit is having 6, so we will find square of which numbers from 1 to 9 are having 6 in the ones digit place which will be 4 and 6. So either 4 or 6 will form the one's digit of the square root of 4096.⇒ Now we will find square of which number from 1 to 9 is the closest to the last two digits of 4096 i.e. 40 which will be 62 = 36. So either 64 or 66 can be the square root of 4096.
⇒ Now multiply this 6 with its next number 7 which will come as 42. As 40 is smaller than 42, hence the smaller number 64 will be the desired square root.
Cube Root:
Cube Root of 19683:
⇒ Here the one's digit is having 3, so we will find cube of which numbers from 1 to 9 are having 3 in the ones digit place which will be 7. So 7 will form the one's digit of the cube root of 19683.⇒ Now 19 falls between the cube of 2 and 3, so the smaller number between 2 and 3 i.e. 2 will form the tens digit of the cube root.
⇒ Hence, the cube root of 19683 will be 27.
==>> Learn Cube Root quick trick here
Quadratic Equations:
a) x2-13x+40=0:
⇒ Here, Product = Coefficient of x2 × constant = 1 × 40=40⇒ Add = (-1) × Coefficient of x = (-1) × (-13)= 13.
⇒ If the product is positive, the sign of the roots will be same and it will depend upon the sign of the Add. So in this case, the sign of the roots will be positive.
⇒ Hence, x = 8, 5
b) x2-x-6=0:
⇒ Here, Product = Coefficient of x2 constant = 1×(-6) = -6⇒ Add = (-1)×Coefficient of x = (-1)×(-1) = 1
⇒ If the product is negative, the sign of the roots will be different and the sign of the bigger root will be similar to the sign of the Add and the sign of the smaller root will be the complementary. So in this case, the sign of the bigger root, 3 will be positive and the smaller root, 2 will be negative.
⇒ Hence, x = 3, -2
==>> Read Quadratic Equations shortcuts here
Compound Interest:
a) C.I. for 2 years, CI2 = R2% × Principal where, R2=2r|r2
Example: Principal = 10,000; Rate = 12%; Time = 2yearsHere, R2 = 2×12|12×12 = 24|144 = 25. 44
⇒ CI2 = 25.44% × 10000 = 2544
b) C.I. for 3 years, CI3 = R3% × Principal where, R3=3r|3r2|r3
Example: Principal = 25,000; Rate = 12%; Time = 3yearsHere, R3 = 3×12|3×12×12|123 = 36|432|1728 = 40.4928
⇒ CI3 = 40.4928% × 25000 = 10123.20
Time and Work
Every question in time and work chapter can be solved easily by finding the efficiency of workers or subject (such as pipes).For example - A takes 10 days to complete a job. B takes 20 days to complete the same job. In how many days they will complete the job if they work together?
⇒ A's efficiency = 100/10 = 10% per day
⇒ B's efficiency = 100/20 = 5% per days
⇒ A and B can do 15% of the work in a day if they work together. So they can do the whole job in 100/15 = 6.66 days or 6 days and 18 hours.
⇒ Detailed post on Time and Work chapter (Practice questions)
In case of profit
25% of Cost Price (1/4 of CP) = 20% of Selling Price (1/5 of SP)
Similarly, 1/3 of CP = 1/2 of SP
In case of loss
25% of Selling Price (1/4 of SP) = 20% of Cost Price (1/5 of CP)
Similarly, 1/3 of SP = 1/2 of CP
Profit and loss practice questions
Let's take an example : 16, 26, 6, 46, -34, ?
There is a pattern in the difference between the numbers in the series.
Every consecutive difference is multiplied by -2.
Similar questions are asked in the exams.
Example - 112 × 92
Simply 112 × 9 = 1008
⇒ Add a zero 10080 and then add 224 to 10080.
⇒ Answer is 10304
You need to do all the calculations in your brain. Don't use paper. You need to divide complex calculations into parts and solve it in your brain without paper. That's how toppers do complex calculations during exams.
Right now it will be difficult for you to use this method but with practice, you will be able to do any complicated calculation within seconds.
Profit and Loss
Profit/loss = Sales price - Cost priceIn case of profit
25% of Cost Price (1/4 of CP) = 20% of Selling Price (1/5 of SP)
Similarly, 1/3 of CP = 1/2 of SP
In case of loss
25% of Selling Price (1/4 of SP) = 20% of Cost Price (1/5 of CP)
Similarly, 1/3 of SP = 1/2 of CP
Profit and loss practice questions
Number Series
In Number series questions, you need to find the pattern of series.Let's take an example : 16, 26, 6, 46, -34, ?
There is a pattern in the difference between the numbers in the series.
Every consecutive difference is multiplied by -2.
Similar questions are asked in the exams.
Estimation
That's the most important technique. This is not a secret that every successful candidate is using this technique during exams.Example - 112 × 92
Simply 112 × 9 = 1008
⇒ Add a zero 10080 and then add 224 to 10080.
⇒ Answer is 10304
You need to do all the calculations in your brain. Don't use paper. You need to divide complex calculations into parts and solve it in your brain without paper. That's how toppers do complex calculations during exams.
Right now it will be difficult for you to use this method but with practice, you will be able to do any complicated calculation within seconds.
Rule of 72, 114 and 142
The rule of 72 is a shortcut technique to estimate the number of years it will take for your money to double with compounding interest.For example: If you are invested Rs. 100, then how much time it will take to double your money, If the rate of interest is 6%?
So, according to rule of 72:
72 ÷ 6 i.e. 12 years.
Read the complete post on Rule of 72, 114 and 144 here
Linear Equations
This technique has been originated from Vedic Maths. This technique willExample
Step 1 - Find Numerator
Cross multiply the coefficient of y with independent terms.
Step 2 - Find Denominator
The denominator is obtained by cross multiplying (4 ✖️ 2) and subtracting from it the cross product of (5 ✖️ -3) as shown below:-
Value of x

For more Concepts and Tricks Click here